코딩 다이어리
경사하강법 본문
경사하강법이란?

- 1차 근삿값 발견용 최적화 알고리즘으로 주로 딥러닝에서 최적의 가중치를 구하기위해 사용
- 함수의 기울기(경사)를 구하고 경사의 절댓값이 낮은 쪽으로 계속 이동시켜 극값에 이를 때까지 반복
- 보통 함수의 최솟값을 찾기 위해 미분계수를 구하지만 머신러닝에서는 거의 사용하지 않음
- 실제 데이터를 사용한 분석에서 함수들의 형태가 복잡해 미분계수와 근을 계산하기 어려움
- 데이터의 양이 많아질 수록 미분계수 계산 과정보다 경사하강법이 효율적
수식 유도 과정
- 함수의 기울기(즉, gradient)를 이용해 x의 값을 어디로 옮겼을 때 함수가 최소값을 찾는지 알아보는 방법
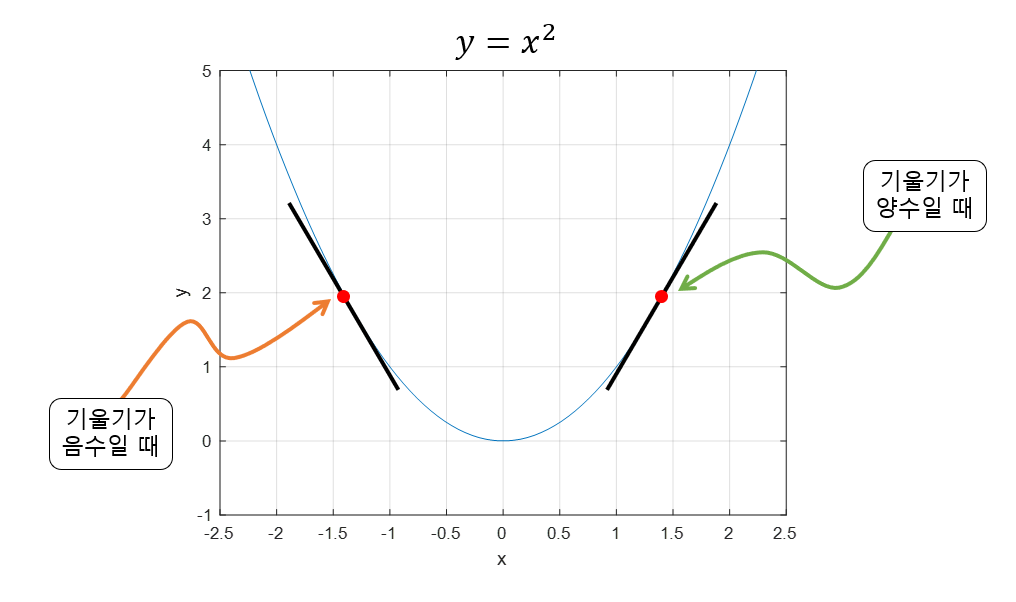
- 기울기가 양수이면 x값이 커질 수록 함수값이 커지고, 기울기가 음수이면 x값이 커질 수록 함수값이 작아짐
- 기울기의 절대값이 크면 가파르며 현재 함수값이 함수의 최솟값이나 최대값으로부터 멀리 떨어져 있음
- 즉, 기울기가 양수이면 음의 방향으로 x를 옮기고, 기울기가 음수이면 양의 방향으로 x를 옮기면 극값을 향하게 됨
- 이를 수식으로 나타내면 아래와 같음
- $ x_{i+1} = x_{i} - 이동거리 \times 기울기의 부호 $
- $ x_{i+1} = x_{i} - \alpha\frac{\text{d}f}{\text{d}x}(x_{i}) $
경사하강법의 한계
1. Local Minima 문제

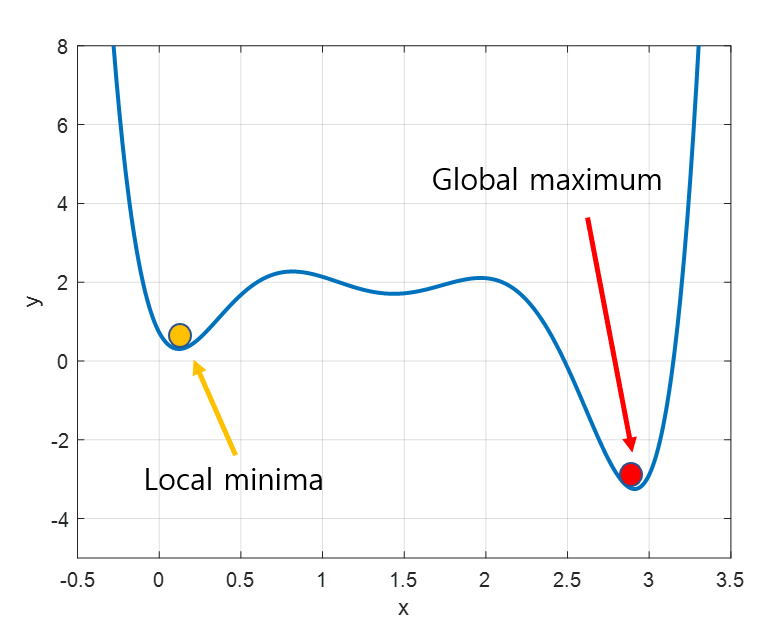
- 함수의 최솟값을 Global Maximum이라고 하며, 경사하강법은 global maximum를 찾아 이때의 x값을 구하고 가중치 값을 업데이트함
- 하지만 왼쪽의 그림처럼 파라미터 공간에 수많은 지역적인 홀이 존재하고 Local Minima를 Global maximum으로 착각하여 잘못된 최적해를 찾게 됨
- 경사하강법의 시작 지점에 따라 다른 최적의 값이 구해지기 때문에 반드시 최적해를 구한다는 보장이 없음
2. Saddle Point 문제

- 기울기가 0이지만 극값이 아닌 지점을 안장점(Saddle Point)라고 함
- 위의 그림을 살펴보면, 검은색 점은 A~B 사이에서는 최솟값(minima)이지만 C~D 사이에서는 최댓값
- 경사하강법은 기울기가 0일 경우 더이상 파라미터를 업데이트하지 않기 때문에 안장점을 벗어나지 못함
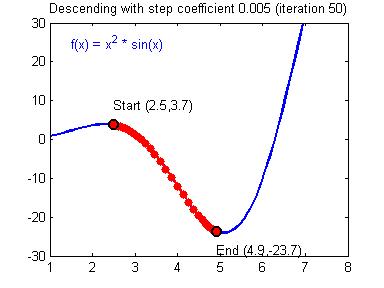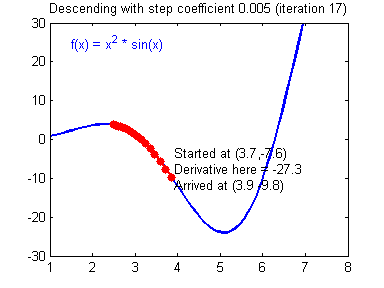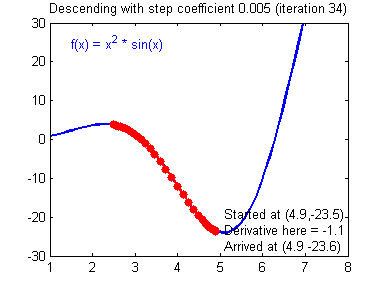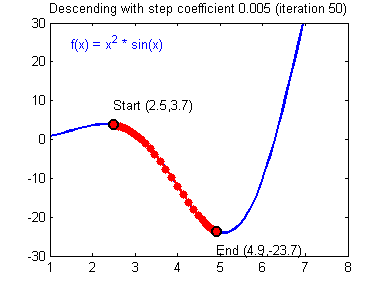
3. Step size 문제

- Step size가 클 경우 한번에 이동하는 거리가 크므로 최솟값에 빠르게 수렴할 수 있지만 오히려 함수값이 커지는 방향으로 최적화가 진행되어 발산하는 경우가 생김
- Step size가 작은 경우 발산할 위험이 적어지지만 최솟값을 구하기 위해 더 많은 시간이 소요됨
- 수렴하지 않거나 발산하지 않도록 적절한 Step size를 조절해야 함
참고사이트
https://angeloyeo.github.io/2020/08/16/gradient_descent.html
경사하강법(gradient descent) - 공돌이의 수학정리노트
angeloyeo.github.io
https://velog.io/@sasganamabeer/AI-Gradient-Descent%EA%B2%BD%EC%82%AC%ED%95%98%EA%B0%95%EB%B2%95
[AI] Gradient Descent(경사하강법)
경사하강법(Gradient Descent)은 1차 근삿값 발견용 최적화 알고리즘이다. 기본 개념은 함수의 기울기(경사)를 구하고 경사의 절댓값이 낮은 쪽으로 계속 이동시켜 극값에 이를 때까지 반복시키는 것
velog.io
'머신러닝 > 딥러닝' 카테고리의 다른 글
| RNN(Recurrent Neural Network, 순환 신경망) (2) | 2023.01.19 |
|---|---|
| CNN (1) | 2022.12.23 |
| 순전파(Foward Propagation)와 역전파(Back Propagation) (0) | 2022.12.18 |
| 활성화 함수(Activation Function) (0) | 2022.12.08 |
| 퍼셉트론(Perceptron) (0) | 2022.12.07 |
Comments




